2022. 1. 8. 17:23ㆍAlgorithm
Union-Find 자료구조 개념
Union-Find는 서로소 부분집합 구조로 나뉘어진 데이터들을 다루는 자료구조입니다.
여기서 서로소 부분집합이란??
수학적으로 표현하면,
{1,2}, {3,4}, {5,6} 과 같이 서로 다른 원소들을 가진 집합들 사이 관계를 의미합니다.
3가지 집합에서 서로 공통된 원소가 없으면 서로소 부분집합이라고 합니다.
그럼 이를 어떻게 구현할까요?
두가지 함수와 한개의 배열로 구현해볼 수 있습니다.
Parent 배열
먼저, 자기 자신을 가리키는 parent 배열 한개를 만들어줍니다.
| 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 1 | 2 | 3 | 4 | 5 |
이 parent 배열은 자신의 부모를 가리킵니다. 처음 시작은 모두 각자 자기자신을 부모로 가지고 있습니다.
findParent(A)
A원소의 부모가 어느 index에 있는지 알려줍니다.
Union(A,B)
A와 B원소를 가진 두 집합을 합쳐줍니다.
어느 쪽이 parent가 될지는 상황에 따라 다릅니다. 작은 숫자로 몰아줄 수 있고, 혹은 큰 숫자쪽으로 몰아줄 수 있습니다.
하지만 이를 자료구조 측면에서 생각해보면 더 큰 집합쪽이 parent가 되는 것이 더 유리합니다.
이 배열은 아래 그림과 같이 결국 트리구조입니다. Parent와 Child구조로 되어있기 때문입니다.
그렇기 때문에 트리의 층 수를 적게 하기 위해서는 작은 쪽 집합을 큰 쪽 집합에 붙여야 합니다.
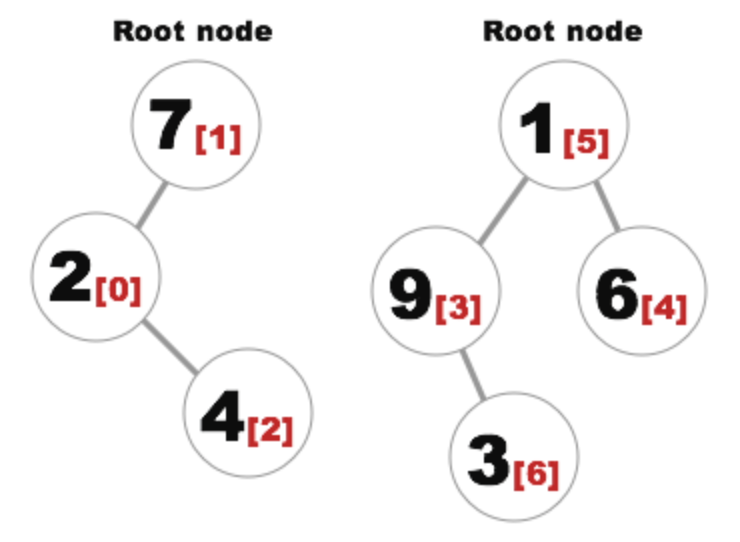

이 Union함수에서 중요한 점은 두 원소의 parent를 찾은 후, 그 parent끼리 비교하여 합치는 것입니다.
parent를 찾지 않고 두 원소를 합치게 된다면 시간복잡도가 최악의 경우 O(N)이 나올 수 있습니다.
parent를 찾고 업데이트 해줌으로 O(1)이 나올 수 있습니다.
위 두 함수를 사용해서 간단한 예시를 들어서 보면 아래와 같습니다.
아래와 같이 6개의 집합이 있습니다.
{0} {1} {2} {3} {4} {5}
먼저 Union(0,1)을 해주면 (이 때 parent가 되는 것은 더 작은 숫자라고 하자.)
{0,1} {2} {3} {4} {5}
가 되고 parent 배열은 아래와 같이도 됩니다.
| 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | 2 | 3 | 4 | 5 |
Union(1,5)를 해주면
{0,1,5} {2} {3} {4}
가 되고 parent 배열은 아래와 같이 변합니다.
| 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | 2 | 3 | 4 | 1 |
여기서 findParent(5)를 해주면,
1 이 나오지만, 1은 parent가 아니기 때문에 한번 더 findParent를 하여 0을 구해야 합니다.
여기서는 재귀함수로 구현해주어야 합니다.
코드 구현
구현한 코드는 아래와 같습니다.
import Foundation
// 1
var parent = [Int]()
for i in 0...10 {
parent.append(i)
}
// 2
func findParent(_ element: Int) -> Int {
if parent[element] != element {
return findParent(parent[element])
} else {
return element
}
}
// 3
func union(_ first: Int, and second: Int) {
let firstParent = findParent(first)
let secondParent = findParent(second)
if firstParent < secondParent {
parent[secondParent] = firstParent
} else {
parent[firstParent] = secondParent
}
}위가 전체 코드이고 분리해서 설명하겠습니다.
// 1
var parent = [Int]()
for i in 0...10 {
parent.append(i)
}parent배열을 만들어 주었습니다.
parent배열을 모두 자기자신을 가리키도록 초기화해주었습니다.
// 2
func findParent(_ element: Int) -> Int {
if parent[element] != element {
return findParent(parent[element])
} else {
return element
}
}findParent함수는 재귀함수로 표현해야합니다.
parent배열은 parent 원소를 가리키도록 저장하지만 위 표에서 5 원소와 같은 경우가 나올 수 있습니다.
parent배열에서 자신을 가리키면 parent를 찾았다고 판단할 수 있습니다.
// 3
func union(_ first: Int, and second: Int) {
let firstParent = findParent(first)
let secondParent = findParent(second)
if firstParent < secondParent {
parent[secondParent] = firstParent
} else {
parent[firstParent] = secondParent
}
}union함수는 두 원소의 집합을 합쳐야 합니다.
findParent를 이용하여 두 원소의 parent를 찾은 후,
parent 대소관계를 비교해서 더 작은 쪽을 parent로 지정해주었습니다.
이 때, 두 parent가 같으면 아무일도 안해줘야 되지만 어차피 같기 때문에 위와 같이 표현해주어도 어차피 아무 상관없습니다.
UnionFind 자료구조를 클래스로 만들기
위와 같이 간단하게 구현해주어도 되긴 하지만,
또 집합 사이즈도 고려한 방식이 무엇이 있을까 찾아보다가 발견한 코드입니다.
위 코드와 다른 점은 두가지 있습니다.1. index 딕셔너리를 통해 원소와 index가 다를 경우 원소에서 바로 index를 찾을 수 있도록 해줍니다.2. size 배열을 통해 union함수에서 parent를 정해줍니다.
struct UnionFind<T: Hashable> {
private var index = [T: Int]()
private var parent = [Int]()
private var size = [Int]()
mutating func addSetWith(_ element: T) {
index[element] = parent.count
parent.append(parent.count)
size.append(1)
}
mutating func setOf(_ element: T) -> Int? {
if let indexOfElement = index[element] {
return setByIndex(indexOfElement)
} else {
return nil
}
}
mutating func setByIndex(_ index: Int) -> Int {
if parent[index] == index {
return index
} else {
parent[index] = setByIndex(parent[index])
return parent[index]
}
}
mutating func inSameSet(_ firstElement: T, and secondElement: T) -> Bool {
if let firstSet = setOf(firstElement), let secondSet = setOf(secondElement) {
return firstSet == secondSet
} else {
return false
}
}
mutating func unionSetsContaining(_ firstElement: T, and secondElement: T) {
if let firstSet = setOf(firstElement), let secondSet = setOf(secondElement) {
if firstSet != secondSet {
if size[firstSet] < size[secondSet] {
parent[firstSet] = secondSet
size[secondSet] += size[firstSet]
} else {
parent[secondSet] = firstSet
size[firstSet] += size[secondSet]
}
}
}
}
}참고
https://victorqi.gitbooks.io/swift-algorithm/content/union-find.html
Union-Find · Swift Algorithm
victorqi.gitbooks.io
'Algorithm' 카테고리의 다른 글
| [Programmers] 문자열 압축 (0) | 2022.02.01 |
|---|---|
| [Baekjoon] 1021 회전하는 큐 (0) | 2022.01.12 |
| [Baekjoon] 10775 공항 (0) | 2022.01.07 |
| [Programmers] 순위검색 (0) | 2022.01.02 |
| [Programmers] 키패드 누르기 (0) | 2021.05.09 |